Solve Sudoku (Without even thinking!)

Sudoku 4 Beginner

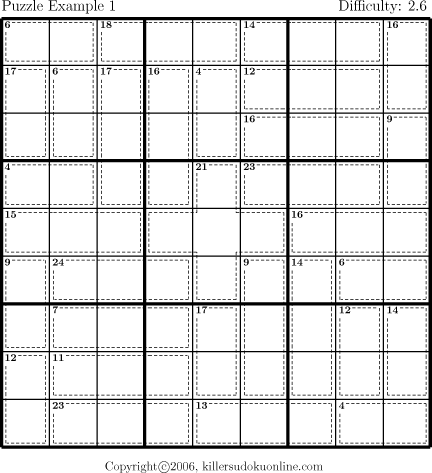
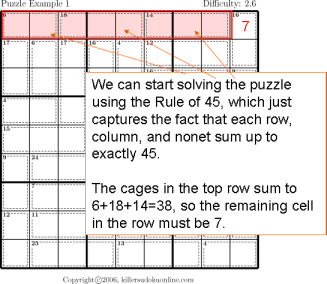
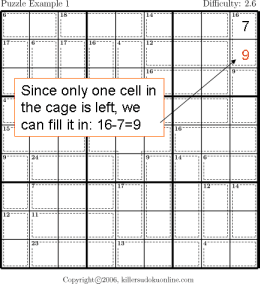
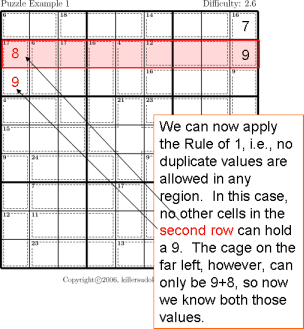
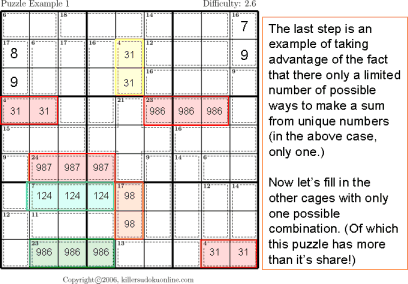
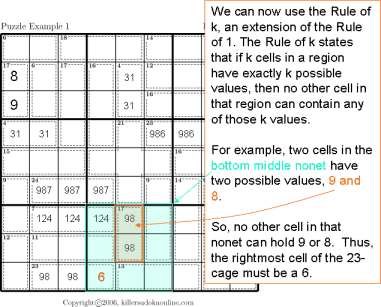
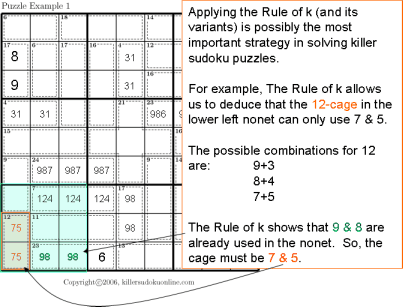
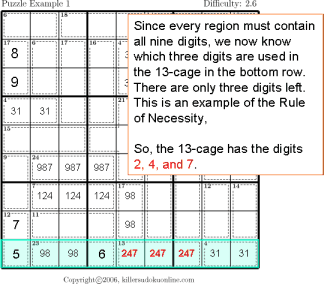
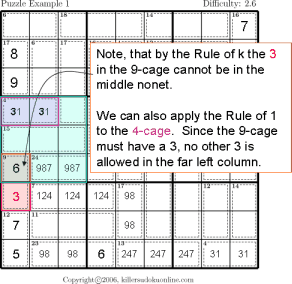
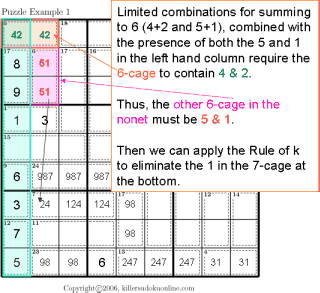
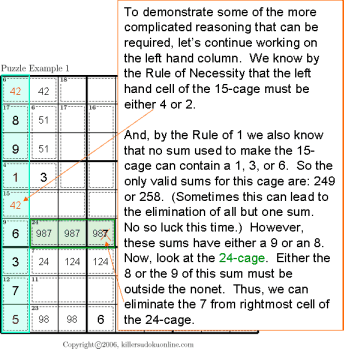
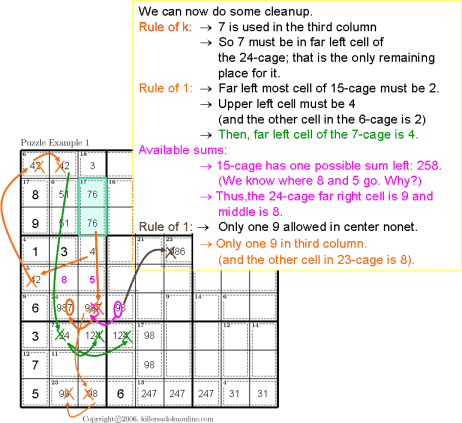
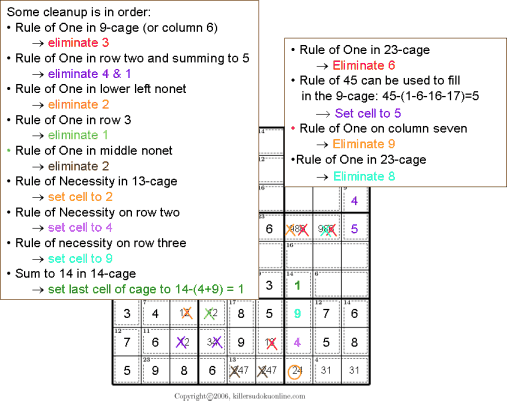
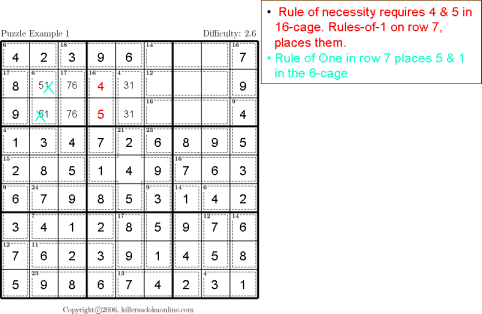
This instructable provides step by step instructions to complete a Sudoku puzzle by simple process of elimination.

One of the things I that drove me crazy about Sudoku is how difficult it is to return to a puzzle if you get interupted. This system allows you to walk away from a puzzle at any time and return exactly where you left off.

Step 1What you need to begin

You need: 

1. A sudoku puzzle. I enlarged this one (which was the puzzle that appeared on Sudoku.com on July 8, 2006.) to make photography easier. I find this system works better on larger puzzles.

2. A pencil, Not a pen. A pencil.

3. An eraser

Step 2Fill in the "Missing Grid"

You see, a Sudoku puzzle is missing a grid. Once you put in this grid, it is sooo much easier. 

Enter the numbers 1 through 9 in a "tic-tac-toe" pattern in every blank box. 

Step 3Erase "Across"

For each number that is preprinted in the puzzle, you will start erasing that number from the appropriate grids you just wrote in.

So the first number (in the upper right corner) is a "6". Erase every other "6" in that row. Once you have completed the erasing, draw a line across the top of the number to indicate that you have cleared out that line
.

Step 4Erase Down

Now, for that same number "6", erase the corresponding "6"'s in every box in the same column. Once you have completed erasing, draw a line down the edge of the number to indicate that you have completed this step

.

Step 5Erase "All Around"

Ok, last step for the first number "6" Erase all the "6"s in the same quadrant. Then draw a circle around the number to indicate you have completed this step.

Now you have eliminated all the sixes from all the other blocks. That indicates that a Six canot appear in any of those blocks.

Keep going, repeat those same three steps for all the other pre-printed numbers in the puzzle

Step 6Repeat for all the pre-printed numbers

Just repeat thos three steps for each number that was printed in the puzzle. The purpose of the down, across, and circle marks on each number is to provide for any interruption that may occur when solving the puzzle. By drawling those lines you can always tell exactly where you left off. If the number has all three marks, you can be sure that all of the corresponding numbers have been eliminated from the puzzle. YOu can effectively forget about that block now.

Let's see what the result of all that erasing was. 

Step 7Locate Answers

By process of elimination you will have done so much erasing in some blocks that only one number is left. Guess what. THat is the answer for that block. Congratulate yourself.

Write that number large in the block, then treat it like a preprinted number. Eliminate all the across, down and around numbers as you have already done so many times before.

In this image, the red pen points point to all the answers that were provided just by doing the initial erasing.

We have not yet begun to think!

Step 8Other kinds of eliminations.

You won't always be so lucky. Not every time will you end up erasing all the numbers but one in a block. If that is the case, then you peruse the puzzle to find eliminations.

First look down each column. If you find a number that only appears in one block in a column. That is the answer for that block.

In this picture, the pen point points to a three. That is the only three in that column, so that must be where it goes.

Write it large, then treat it like a pre-printed number. See ... this isn't thinking. This is EASY

Step 9Look Around a quadrant.

I know, they aren't really quadrants, but you know what I mean, don't you?

If you've looked across the columns, and across the rows and there are all duplicates, then look in the group. If there is one number in the group that only appears in one block, then it's your answer.

See... There is no guessing in Sudoku. One of these situations has to occur. You just need to find them.

IN this picture the 5 only appears in one block in the group. It goes there.

Write it big, then treat it like a pre-printed number.

See where we're going, here?

Step 10Lather, rinse repeat.

Eventually, you will find all those lonely numbers in thier rows, columns or groups.

Remember to draw those lines and circles in case you get interrupted.

Eventually you will solve the puzzle.

Compare our solution to the "Official Solution" found on the Sudoku.com site. See? A perfect match.

And you thought Sudoku was hard.

It's so easy, you don't even have to think!

Sudoku 4 Beginner

Read more »

Sudoku 4 Beginer

I will be showing the most basic to not so basic methods,trick and tips to finish a sudoku.this instructable is for anyone who plays or wants to play sudoku even if you don't know how to play.

I'll start with the basic thing and progress to the less basic things.

Step 1How to play sudoku

The objective is to fill a 9x9 grid so that each column, each row, and each of the nine 3x3 boxes (also called blocks or regions) contains the digits from 1 to 9.

A cell is the smallest block in the game. A row , column and region consists of 9 cells and the whole game consists of 81 cells. A region has thicker lines surrounding it. This simply makes it easier to play the game
.

Step 2The basic basics(scanning)

I most basic strategy to find missing numbers is scanning and it consists of
1)Cross-hatching.
2)Counting.

1) Crosshatching (shown in the first picture). You scan rows and columns to eliminate where a specific number can be in a given region.As you can see there is only one legal place left for the 1(marked green).

2)Counting. In counting you simply count all the different numbers that's in a row,column and region that connects to one cell. if there is just one number missing then thats what should be in the cell. Take a look at the second picture and see if you can figure out the missing number in the green cell.

the correct answer is :4

legend: green = result
red = cause(the cause of the result that is
)

Step 3The analysis is a higher level method

Analysis consists of two methods namely candidate elimination and the what if. 

I will not be showing the what if to you because i don't like it. It's slow progress and i don't like to erase that much. 

the candidate elimination. the method for candidate elimination I'm showing now is the matched pair method.This method happens when a pair of numbers are the only possible answer to two cells. 

Take a look at the picture. I have concluded(with the help of cross hatching) that 7 and 8 can only be in two places in the lower left region(i filled both in) . The two cells which 7 and 8 can be in is in the same column, thus it cannot be elsewhere in the column. There is two other blank cells in this column and the missing numbers is 9 and 3. We can see that 3 can not be in the 'middle' open cell. This means 3 is in the top cell(marked green) and 9 is in the 'middle' cell. 

Candidate elimination can also be used with three number in three cells. 

*note: Candidate elimination is note the fastest nor easiest method for for finding the green cells answer. That is why one must first scan before analyzing . I will try to find a better example
.

Step 4Analysis (almost , I think)

this one is almost like the candidate elimination i showed you in the previous step(its called deriving certainty from uncertainty).

Take a look at the picture below.In the center region. There is only two possible places for the 7(and 2). There is three places for the seven in the middle right region , but can not be in the middle ones because 7 is reserved by the center region thus there is only one place let for the seven in the middle right region
.

Step 5Xy-wing(This is an advanced technique )

he xy wing is the most difficult technique i have tried because its more difficult to spot it(and to teach :-)

You'll understand better if you check the pics. It works by removing candidates.

the values in the blue squares will be assigned an x,y,z according to the numbers. In this instructable x=8 ; z=2 ; y=9 The green square with the redlining around it is a buddy(in the same row,column or region) of the blue block with 8,9 and the blue block 8,2. and the 9,2 blue block is an buddy of the 8,9 and 8,2 blue blocks. This means that 8(which is also in the two blue buddy blocks). cannot be in the red lined block. If your not sure why check the next picture.
 

Step 6Software

i have used a few programs to play sudoku with and only one has made it mark. It's called simple sudoku. The things i like about it is the hints and the show candidates feature. The hint tells you the method to use not the number. And the show candidates feature show all the possible answer for each block and you can remove any candidate from a cell.

*note the method for filling in the possible answers is exactly the same as step 1.It is just repeated for each square and written in.

Step 7Lastly(just a small thanks)

Thanks for reading my instructable, If you have any questions or know bout any technique i haven't included please add a comment. I believe I didn't copy anything directly from a site and i you spot that i have then i will rectify the problem. I used wikipedia,simple sudoku and brainbashers for information.

Read more »

'Killer Samurai' Sudoku

Killer Samurai Sudoku is a combination of Killer Sudoku and Samurai Sudoku. They are merged together to create a challenging variation of Sudoku for the many sudoku addicts who want to solve more challenging puzzles. 

Killer Samurai Sudoku Rules

Killer Samurai is an advance variation of Sudoku. Before undertaking a Killer Samurai Puzzle it is very advisable to have a go at solving a Killer Sudoku puzzle as Killer Samurai is almost identical to killer sudoku except it comprises of 5 interlocking killer sudoku grids. If you can solve a killer sudoku puzzle then there is a good chance you can solve these puzzles. As a quick review the rules are as followed:

In each coloured area there is a small number. This represents the total of all the numbers in that coloured area. To solve the puzzle you must make sure that every column, row and every 3x3 box in each larger 9x9 grid contains the numbers 1 through to 9.

A few tips to bear in mind: Remember that there is often a limited combinations for each area. For instance if there are two cells in a coloured area that total up to 5 then there is only two combinations. That of 1 and 4 or 2 and 3. The other tip which is very useful for starting a puzzle is to remember that each 3x3 area totals up to 45. This means that if all the coloured groups are all contained in a 3x3 area except for 1 square. Then that square can be worked out. Because if you total those coloured areas and then minus 45 then you will have calculated the value that must go in the square sticking out of the 3x3 area. (Hopefully I will be able to write some tutorials on solving a Killer Samurai Puzzle soon.).

Colour Killer Samurai Sudoku Puzzles

Answer

Read more »

Killer Sudoku

Basic Solving Strategies

The following are the basic rules used to solve killer sudokus.

Rule of 1

This comes directly from the definition of sudoku. No region can contain any duplicate digits. In a sudoku region each digit appears exactly once. For example, if a digit appears in a row, it cannot be in any other cell in the row. Likewise, each digit can appear in a cage only once. If a digit is in a cage, it cannot appear in that cage again.

Rule of Necessity

This rule can be applied to sudoku regions (i.e., row, column, or nonet) or to a cage. In the former case, each region must contain all the digits one to nine. Thus, if all the digits but one appear in a row, the missing digit must appear in the empty cell.

Rule of 45

Each sudoku region (i.e., row, column, or nonet) contains the digits one through nine. Thus, each sudoku region has a total value of 45. If S is the sum of all the cages contained entirely in a region, then the cells not covered must sum to 45-S.

Rule of K

The Rule-of-k is an extension of the Rule-of-1. If there are k cells contained entirely in a region that contain exactly k different possible values, then no other cell in that region can contain any of those k values.

Sum Elimination

This strategy examines the different possible ways of making the sum of a cage. Reducing the number of different possible ways of making a sum, can often lead to a potential solution. There are many ways of reducing the number of sums. For example, if a 2-cage has a total of 3, 4, 16, or 17 there is only one combination of values that can be used. (3=2+1, 4=3+1, 16=9+7, and 17=9+8.) 3-cages with only 1 combination are: 6=1+2+3, 7=1+2+4, 23=9+8+6, 24=9+8+7. The sum calculator found in the online player page can be very handy.

more to come..go here for 

Applying the basic strategies. An Example

Here we will use the above strategies to solve a puzzle. You might want to print out the puzzle so you can follow along all the steps.

Rule of 45
Rule of necessity
Rule of 1
Unique Sums
Rule of K
Rule of K Limited possible sums
Rule of necessity
Limited Possible Sums
Rule of K
Limited Possible Sums Rule of 1 Rule of K
Rule of Necessity Rule of 1 All Possible Sums
Rule of Necessity Limited possible sums
Rule of K Rule of 1 Limited Possible Sums
Remaining sum Rule of 1 Rule of K Rule of necessity
Sum Elimination
Sum elimination Rule of 1
Range of Totals Sum Elimination
Rule of 1 Rule of necessity Remaining Sum
Limited possible sums Rule of 1 Rule of necessity
Rule of necessity Rule of 1

Sample Sum, You try...

Read more »